Sea f continua en [a,b] y derivable en (a,b),
![]()
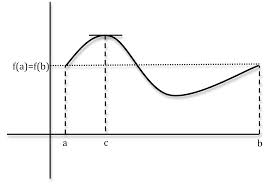
Demostración. Sea h = f(a) = f(b)
Caso 1. Si f(x) = h en [a,b] entonces f es constante y f’(x) = 0 en (a,b)
Caso 2. Si f(x) > h en algún x en (a,b), hay un máximo, M, en el intervalo (a,b)
(Tma. Bolz-W) M > h, entonces
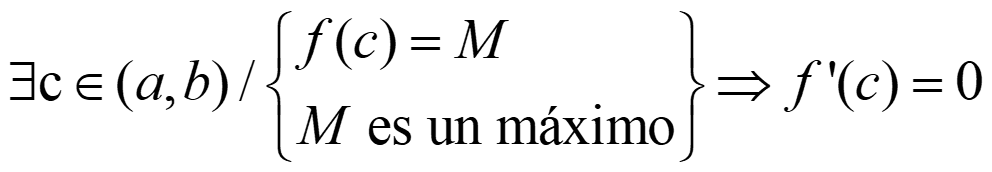
Caso 3. Si f(x) < h análogo al caso 2 QED
Ejercicio. Sea la función f(x) = 2 - |x|. Como puedes ver f(-2) = f(2) pero no existe ningún c en el intervalo (-2,2)/ f'(c) = 0. Justifica porque no contradice el Teorema de Rolle
Solución: Porque f no es derivable en x = 0