GRÁFICA DE UNA FUNCIÓN
1. Dominio
Si hablamos de funciones reales con variable real:
–El dominio de una función polinómica es siempre R.
–Tenemos que eliminar las raíces del denominador de una función racional de su dominio.
–El dominio de una función irracional f(x) = √R(x) es Dom f = {x,R(x)≥ 0}
–El dominio de una función logarítmica f(x) = loga L(x) es Dom f = {x,L(x)> 0}
2. Continuidad y derivabilidad
3. Simetría
Una función es par si f(-x) = f(x), es decir, si la gráfica es simétrica respecto al eje Y.
Una función es impar si f(-x) = -f(x), es decir, si su gráfica es simétrica respecto al origen.
4. Periodicidad
Una función se dice que es periódica con período T si, para algún valor constante no nulo T, tenemos: f(x + T) = f(x) para todos los valores de x. Si existe al menos una constante positiva con esta propiedad, se le llama período. Una función con período T se repite en intervalos de longitud T, a estos intervalos también se les conoce como períodos.
5. Puntos de corte con los ejes. Para encontrarlos debemos resolver los sistemas:
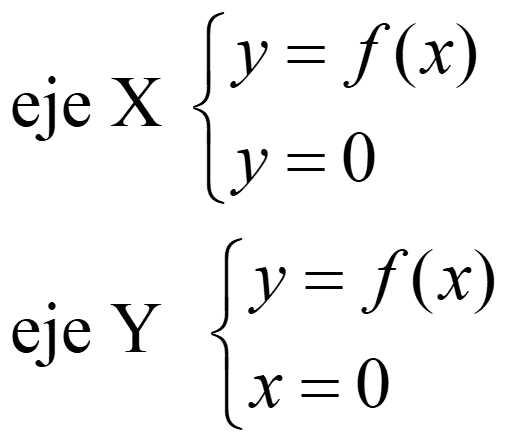
6. Asíntotas
Para encontrarlas, debemos calcular los siguientes límites:
–Asíntotas horizontales:
![]()
–Asíntotas verticales:
![]()
-Asíntotas oblicuas:
![]()
![]()
–Debemos buscar las asíntotas verticales en las raíces de Q(x).
–Cuando grado P < grado Q, hay una asíntota horizontal y = 0
–Cuando grado P = grado Q, hay una asíntota horizontal
–Si grado P = grado Q + 1, hay una asíntota oblicua
7. Extremos, crecimiento y decrecimiento
Se dice que una función es creciente en un intervalo si, para todo x1 y x2 en el intervalo tal que x1 < x2, entonces f(x1) < f(x2).
Una función se dice que es decreciente en un intervalo si, para todo x1 y x2 en el intervalo tal que x1 < x2, entonces f(x1) > f(x2).
El máximo y el mínimo de una función, llamados conjuntamente extremos, son el mayor y el menor valor que toma la función en cada punto de un entorno dado (extremo relativo) o en todo el dominio (extremo absoluto).
Si f es derivable en (a,b):
–f es creciente en (a,b) ↔ f’(x) > 0
–f es decreciente en (a,b) ↔ f’(x) < 0
f tiene un extremo relativo en c → f’(c) = 0
NOTA: los candidatos a ser extremo relativo son cЄR/ f’(c) = 0 o aquellos en los que f no es derivable
8. Curvatura y puntos de inflexión
Para Estudiar la curvatura de una función derivable, hay que estudiar los intervalos en los que la función es cóncava hacia arriba o cóncava hacia abajo.
- f es cóncava hacia arriba en c si la gráfica está por encima de la recta tangente a la curva en c.
- f es cóncava hacia abajo en c si la gráfica está por debajo de la recta tangente a la curva en c.
Un punto de inflexión es un punto de la curva en el que la curvatura cambia.
Si f es derivable en (a,b)
–f es cóncava hacia arriba en (a,b) ↔ f’’(x) > 0
f tiene un punto de inflexión en c → f’’(c) = 0

9. Gráfica
Teorema de Rolle. Sea f continua en [a,b] y derivable en (a,b),
![]()

Teorema del valor medio de Lagrange, Si f es continua en [a,b] y derivable en (a,b), entonces
![]()

Regla de L'Hôpital. Sean f y g funciones derivables en un intervalo abierto centrado en x = a, si:
