Para Estudiar la curvatura de una función derivable, hay que estudiar los intervalos en los que la función es cóncava hacia arriba o cóncava hacia abajo.
- f es cóncava hacia arriba en c si la gráfica está por encima de la recta tangente a la curva en c.
- f es cóncava hacia abajo en c si la gráfica está por debajo de la recta tangente a la curva en c.
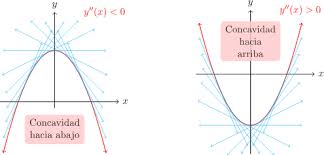
Un punto de inflexión es un punto de la curva en el que la curvatura cambia.
Si f es derivable en (a,b)
–f es cóncava hacia arriba en (a,b) ↔ f’’(x) > 0
–f es cóncava hacia abajo en (a,b) ↔ f’’(x) < 0
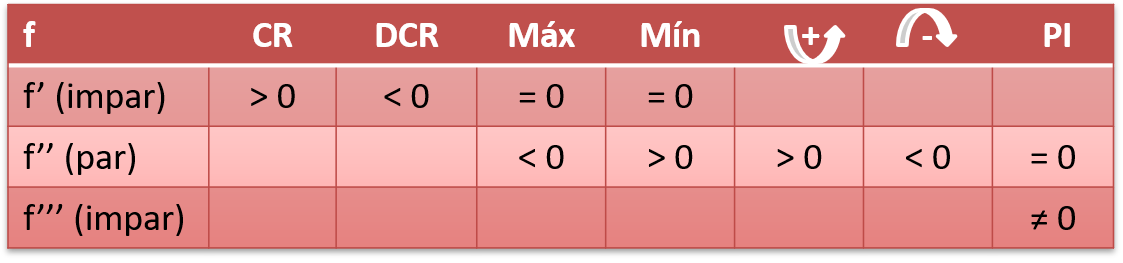
Si f es derivable en cЄR, entonces:
f tiene un punto de inflexión en c → f’’(c) = 0
Ejercicio. Estudia la curvatura de la función y = x·ex y encuentra sus puntos de inflexión
Solución: Punto de inflexión (-2, -2/e2); cóncava hacia arriba (-2,∞); cóncava hacia abajo (-∞,-2)