El límite de una función f, cuando x tiende a c es L si f(x) puede estar tan cerca de L como queramos haciendo que x esté lo suficientemente cerca a c:
![]()
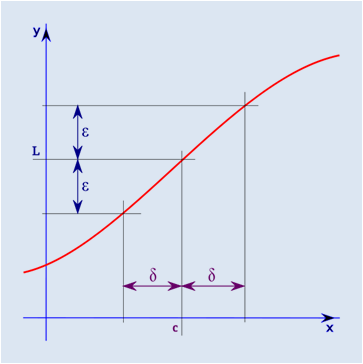
o
![]()
Por ejemplo:
![]() porque
porque

No siempre encontramos el mismo límite cuando nos acercamos por los dos lados, por esto definimos los límites laterales:
- El límite por la izquierda cuando x tiende a c es L-, puede estar tan cerca de L- como queramos haciendo que x esté lo suficientemente cerca a c por la izquierda:
![]()
- El límite por la derecha cuando x tiende a c es L+, puede estar tan cerca de L+ como queramos haciendo que x esté lo suficientemente cerca a c por la derecha:
![]()
![]()
En el ejemplo:
![]()
Otras definiciones:
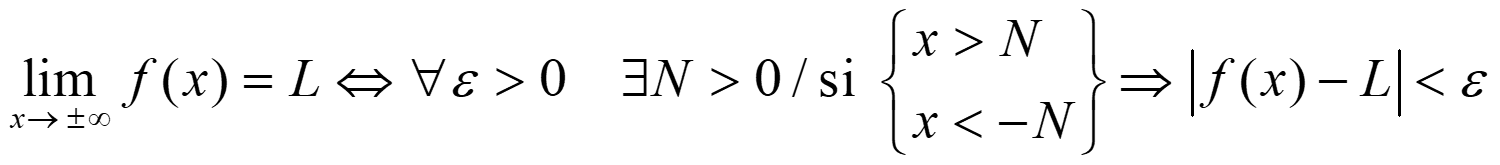
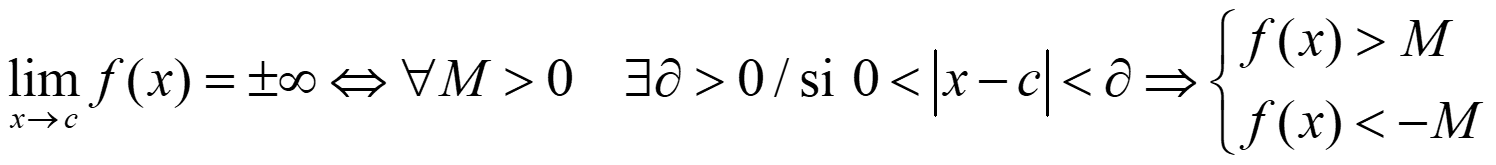
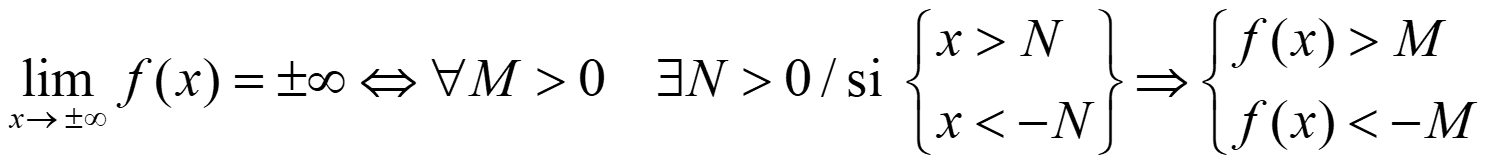
NOTA. Recuerda que cuando
![]()
tenemos una asíntota vertical en x = c
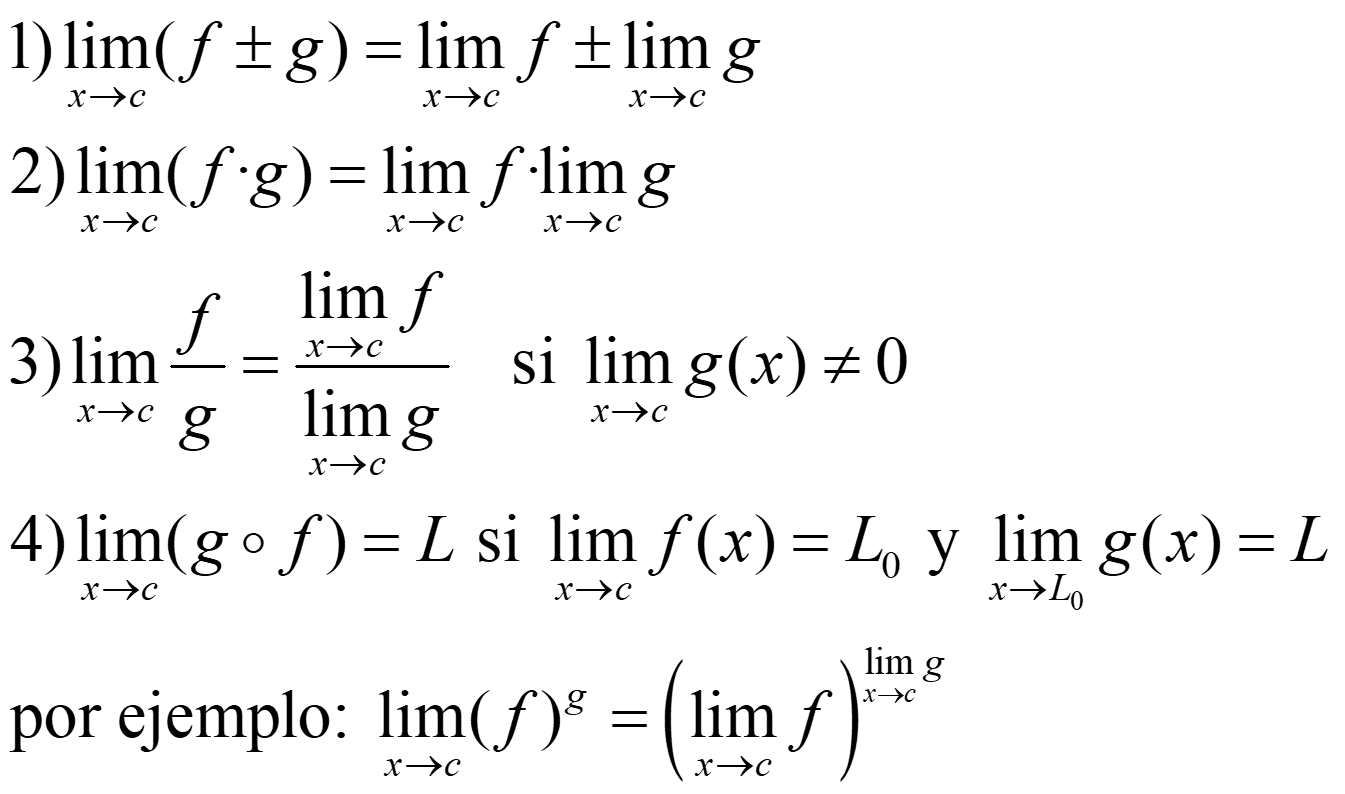
Demostración: Imagina que tenemos dos límites: L y L’ con L ≠ L’. Entonces:
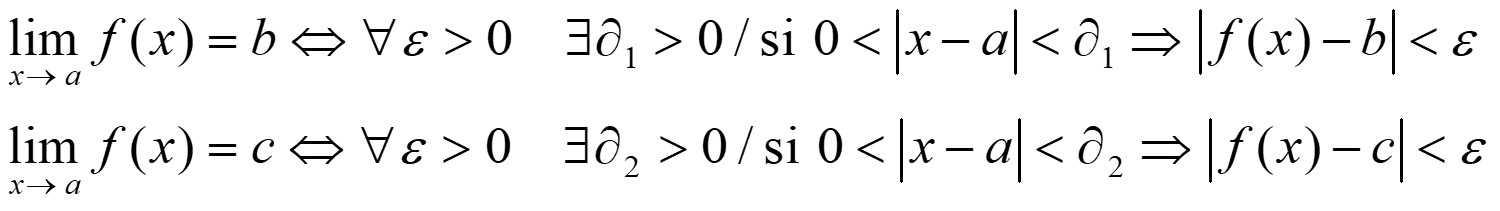
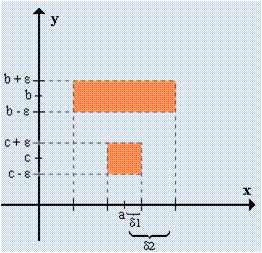
Si elegimos ε como en la imagen hay una contradicción en b usando δ1. Entonces b = c y el límite es único.
Ejercicio. Calcula el límite de f cuando x tiende a 0 y a 2, si:

Soluciones
![]()