De una población extraemos muestras de tamaño n, cada una con su propia media. Sea Xn la variable aleatoria que une cada muestra con su media. Podemos estudiar su distribución denominada distribución muestral de la media.
Cuando una población tiene cualquier distribución, usamos el:
Teorema central de límite. Si cogemos una muestra aleatoria simple de tamaño n de una variable aleatoria de media μ y desviación típica σ (n suficientemente grande, n ≥ 30), la distribución de probabilidad de la media Xn se aproxima a una distribución normal:
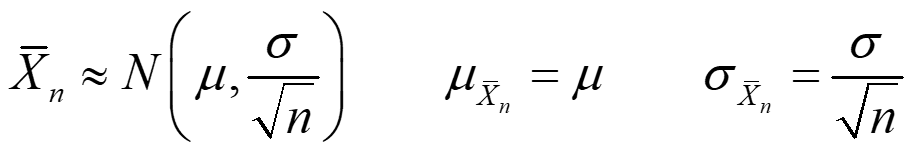
A σXn se le llama error típico.
Si tenemos una distribución normal N(μ,σ), entonces tenemos la misma situación:
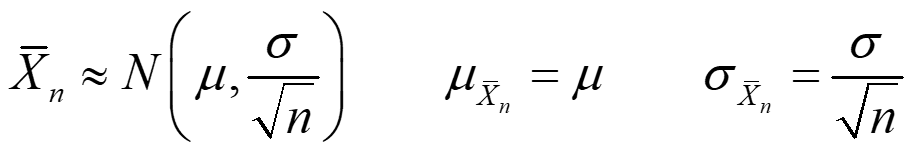
Generalmente, la desviación típica de la población es desconocida. Entonces, aproximamos este parámetro usado la desviación típica de la muestra, si n es suficientemente grande (n ≥ 100).
Ejemplo. Las alturas de 1200 estudiantes de un instituto se distribuyen siguiendo una normal de media 1,72 y σ = 0,09 m. Si tomamos 100 muestras de 36 estudiantes cada una, calcula:
a) La media y desviación típica esperada en la distribución muestral de la media.
b) ¿En cuántas muestras cabría esperar una media entre 1,68 y 1,73 m?
c) ¿En cuántas muestras es de esperar que la media sea menor que 1,69 m?
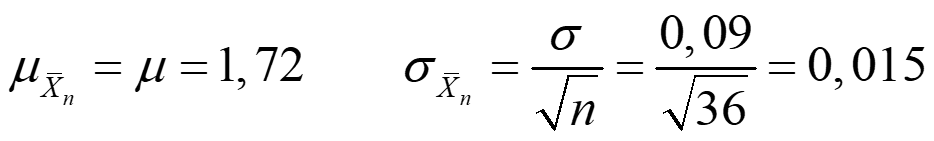
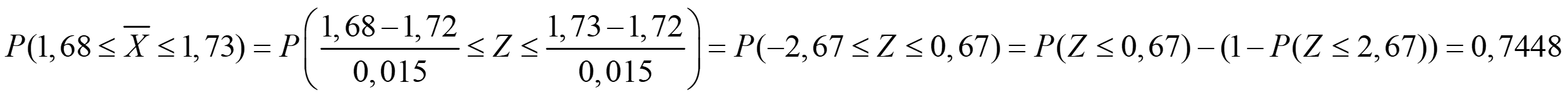
Entonces, el número de muestras es: 0,7448·100 ≈ 74 muestras
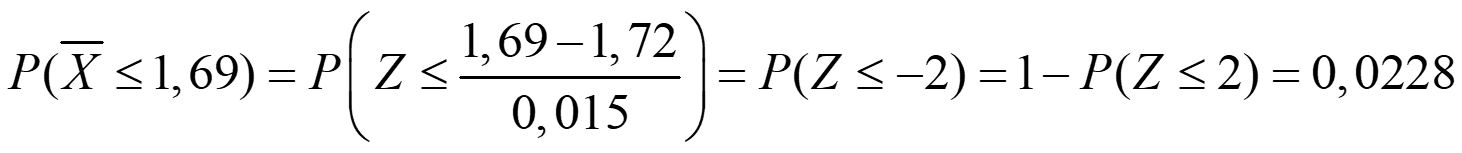
Ejercicio. En la población, el cociente intelectual (CI) se distribuye normalmente con media 100 y desviación típica 15. Si sacamos varias muestras de 25 individuos de la población y medimos su CI, ¿cuántas muestras se espera que tengan la media entre 95 y 105?
Solución: 22,61≈ 23 muestras