Saltar la navegación

Resumen

Una sucesión es un conjunto ordenado de números generados de acuerdo a una regla. Es una función  s: N → R
Cada número de la sucesión se llama término, y los representamos como ai. Llamamos término general de la sucesión, an, a la expresión que representa a cada término de la sucesión.
Algunas sucesiones son recurrentes, porque cada término se obtiene de los anteriores
Una progresión aritmética es una sucesión en la cual la diferencia entre dos términos consecutivos se mantiene constante. Esa constante se llama diferencia de la progresión.
Una progresión geométrica es una sucesión que cumple que el cociente entre dos términos consecutivos se mantiene constante. A esa constante se le llama razón de la progresión.
Un sucesión se dice que converge si existe un número L tal que no importa lo cerca que esté an de L, encontramos un número natural k, tal que los términos {ak, ak+1, ...} son cercanos a L.

 Entonces se dice que la sucesión es convergente y L es su límite,     

En caso contrario, se dice que  la sucesión es divergente.

Propiedades:

 

Nota:

Las sucesiones polinómicas siempre divergen a ±∞, dependiendo del signo del coeficiente del término de mayor grado
Las indeterminaciones son límites que son diferentes dependiendo de cada situación. Son:

Las sucesiones racionales siempre son indeterminaciones, que se resuelven dividiendo todo por el grado más alto
NOTA. Como has comprobado:

Si tenemos sucesiones irracionales, tenemos que hacer la raíz del límite. Siempre divergen si existe. Si son racionales miramos los grados
Podemos encontrar indeterminaciones en la resta de raíces, entonces usamos su conjugado para resolverla
Si hay potencias, usamos las propiedades:

El número e es el límite de la sucesión:

que es una indeterminación del tipo 1∞. Usamos este número para resolver este tipo de indeterminaciones

El límite de una función f cuando x tiende a c es L  si f(x) puede estar tan cerca de L como queramos haciendo que x esté lo suficientemente cerca de c.

Se escribe:

No siempre encontramos el mismo límite si nos acercamos por lados diferentes, por eso definimos los límites laterales:
– El límite de f cuando x tiende a c por la izquierda es L- si f(x) puede estar tan cerca de L- como queramos x haciendo que x esté lo suficientemente cerca de c por la izquierda:

- El límite de f cuando x tiende a c por la derecha es L+ si f(x) puede estar tan cerca de L+ como queramos x haciendo que x esté lo suficientemente cerca de c por la derecha:

Entonces, la función tiene límite en c si y solo si los limites laterales existen y son iguales:

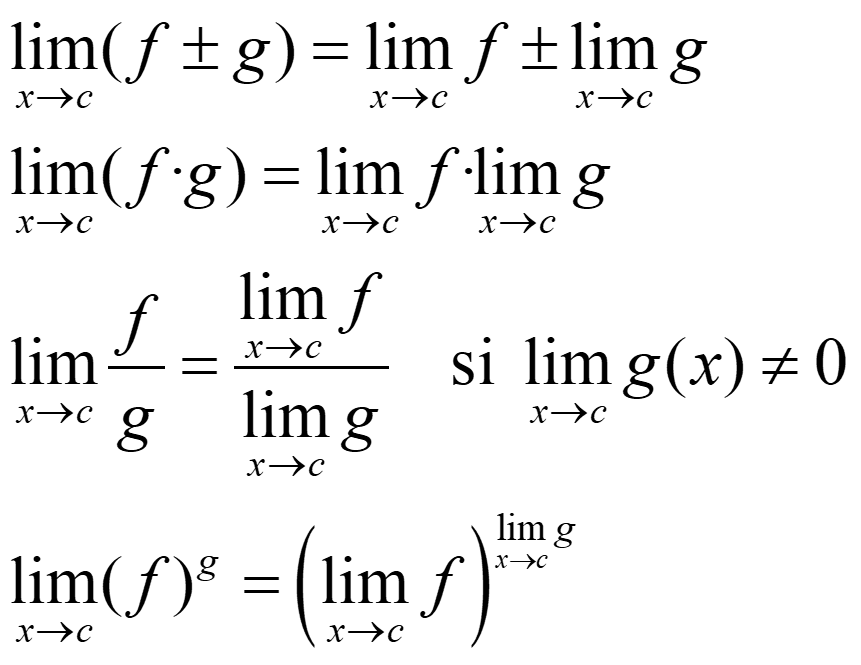
Los límites tienen las mismas propiedades que los de la sucesiones:

Para calcular límites cuando c es ∞, hacemos como en las sucesiones. Si c es -∞, cambiamos:

Para calcular las asíntotas de una función hemos de calcular estos límites:
– Asíntotas horizontales:

- Asíntotas verticales:

- Asíntotas oblicuas:

NOTA: si tenemos una función racional

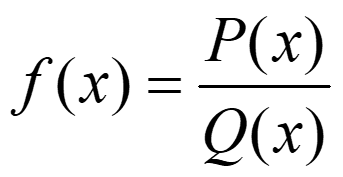
–Buscamos las asíntotas verticales en las raíces de Q(x).
–Cuando grado P < grado Q, hay asíntota horizontal en   y = 0 
–Cuando grado P = grado Q, hay asíntota horizontal
–Cuando grado P = grado Q + 1, hay asíntota oblicua
Una función f se dice que es continua en x = a si :

En caso contrario, se dice que f es discontinua.
NOTA: las propiedades son las mismas que las de los límites.
Hay diferentes tipos de discontinuidades:
– Discontinuidad evitable: si el límite existe pero no es igual a f(a).

– Discontinuidad inevitable: cuando existen los límites laterales y no son iguales. Puede ser salto finito o infinito
            

– Discontinuidad de 2ª especie: cuando no existe uno de los límites laterales.

Creado con eXeLearning (Ventana nueva)