Sea f una función, se dice que F es una primitiva de f si F’ = f.
NOTA. Si F es primitiva de f →F + k (k Є R) es una primitiva de f.
La integral indefinida de f es el conjunto de primitivas de f:
![]()
Ejemplo. 1) ∫cosx dx = senx + k; k Є R
PROPIEDADES:
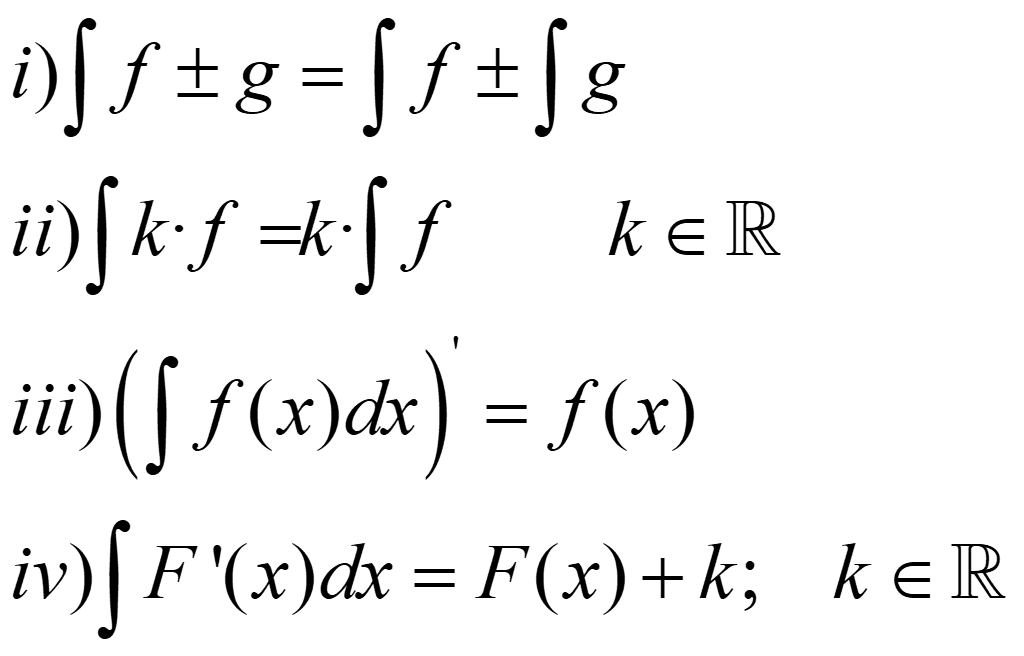
Ejemplos:
2) ∫3 senx dx =3 ∫senx dx = -3 cosx + k k Є R
3) ∫(ex+3)dx = ex + 3x + k k Є R
Ejercicio. Resuelve:
a) ∫3x2 dx =
b) ∫2senx·cosx dx =
Soluciones: a) x3 + k; b) sen2x + k