Resumen
Una función f, es una relación entre dos conjuntos de modo que cada elemento del primer conjunto está relacionado con exactamente un elemento del segundo.
f:X→ Y, X es el conjunto inicial e Y el conjunto final
x →y = f(x) x se llama variable independiente (variable) e y se llama variable dependiente. f(x) es la imagen de x.
Hay 4 maneras de expresar una función:
- Verbalmente, como en los ejemplos anteriores
- Algebraicamente, con una fórmula.
- Con una tabla.
- Con una gráfica.
Si hablamos de funciones reales de variable real:
– El dominio de una función polinómica es siempre R.
– Tenemos que quitar las raíces del denominador de una función racional de su dominio.
Una función es par si f(-x) = f(x), es decir, es simétrica respecto al eje X:
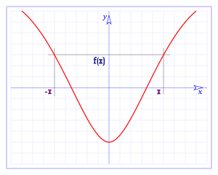
Una función es impar si f(-x) = -f(x), es decir, es simétrica respecto al origen:
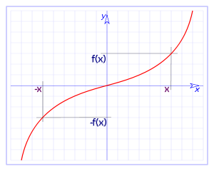
Para encontrar estos puntos gráficamente, tenemos que buscar las coordenadas de los puntos de intersección entre la gráfica y los ejes.
Para hacerlo algebraicamente, tenemos que resolver los sistemas:

Intuitivamente, una función continua es una función que podemos dibujar de un solo trazo. En otro caso, se dice que la función es "discontinua“.
Una función se dice que es creciente en un intervalo si, para todo x1 y x2 en el intervalo tal que x1 < x2, entonces f(x1) < f(x2).
Una función se dice que es decreciente en un intervalo si, para todo x1 y x2 en el intervalo tal que x1 < x2, entonces f(x1) > f(x2).
El máximo y mínimo de una función, llamados colectivamente extremos, son el mayor y el menor valor que la función toma en un punto, bien en un entorno dado (extremo relativo) o bien en todo el dominio de la función (extremo absoluto).
La tasa de variación de una función f en un intervalo [x1,x2] es: TV = f(x2) – f(x1)
La tasa de variación media de una función f en un intervalo [x1,x2] es
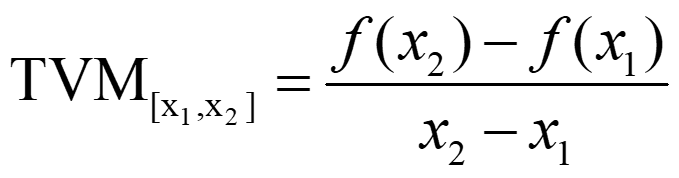
Si f es decreciente en el intervalo→ TVM < 0
Si f es creciente en el intervalo→ TVM > 0
Si f es constante en el intervalo →TVM = 0
Las funciones lineales o afines son de la forma: ![]()
m es la pendiente de la recta
n es la ordenada en el origen
La gráfica de cualquier función lineal es una recta. Si m > 0 es creciente y si m < 0 es decreciente.
Si n = 0, se llaman funciones de proporcionalidad directa:
![]()
La pendiente, m, se llama constante de proporcionalidad. Su gráfica es una recta que pasa por el origen.
Si m = 0, se llaman funciones constantes:
![]()
No es creciente ni decreciente. Su gráfica es una recta paralela al eje X.
Las funciones cuadráticas son de la forma: ![]()
La gráfica de la función es una parábola. El vértice de la parábola se encuentra en el punto de abscisa x =-b/2a y su eje de simetría es la recta de ecuación x = -b/2a.
La función tiene un máximo absoluto y relativo en el vértice si a < 0 y un mínimo absoluto y relativo si a > 0.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 3.0